Chapitre 8 Distances au-delà du système solaire

Au chapitre précédent nous avons discuté de la façon dont les télescopes nous permettent de collecter la lumière afin de l’analyser et d’en extraire le maximum d’information sur les astres. Une des questions les plus naturelle qu’on peut poser à propos des astres et à laquelle on pourra répondre en utilisant les données collectées par les télescopes, c’est de se demander à quelles distances ils se trouvent de nous. Les distances dans l’Univers sont si grandes que les évaluer est une tâche remarquablement difficile. Nous avons déjà discuté des méthodes utilisées pour évaluer les distances dans le système solaire. Le premier jalon était la mesure de la taille de la Terre par Ératosthène. Cette mesure avait ensuite permis de déduire la valeur de l’unité astronomique et donc d’établir les distances des différents objets dans le système solaire grâce à des méthodes géométriques, comme celle de la parallaxe. Ces valeurs ont été confirmée par la méthode du radar. L’objectif de ce chapitre est d’explorer les étapes suivantes dans l’échelle des distances cosmiques. Nous ne présenterons qu’un petit nombre de méthodes, il en existe plusieurs autres que nous n’aurons pas le temps d’aborder.

Méthode de la parallaxe

Nous avons vu au chapitre 4 que la méthode de la parallaxe consiste à observer un objet de deux points de vue différents. On voit alors l’objet à deux endroits différents par rapport aux étoiles lointaines et en faisant un peu de trigonométrie, on peut déduire la distance de l’objet. Cette technique fonctionne bien si on on a deux points de vue assez éloignés l’un de l’autre. Par exemple, nos deux yeux, séparés d’environ 10 cm, nous permettent d’évaluer des distances de l’ordre de quelques mètres. En observant de Paris et Cayenne, deux villes séparées de 7 000 km, Cassini et Richer ont été en mesure de déterminer la distance de Mars, situés à environ 100 millions de km de la Terre. Cependant, si on veut mesurer la distance d’objets à l’extérieur du système solaire, les deux points d’observation doivent être encore plus éloignés l’un de l’autre.

Le premier astronome a avoir appliqué la méthode de la parallaxe pour mesurer la distance d’une étoile est Friedrich Bessel (1784-1846). L’idée ingénieuse qu’il eut fut de mesurer la parallaxe de l’étoile en l’observant à six mois d’intervalle. En six mois, la Terre fait la moitié d’une révolution autour du Soleil ce qui fait qu’on a deux points d’observation qui sont séparés par le diamètre de l’orbite terrestre. Connaissant ce diamètre (2 unités astronomiques), Bessel a été en mesure de déduire que l’étoile 61 Cygni était à une distance de 10,3 années-lumière (la valeur aujourd’hui acceptée est 11,4 années-lumière). Pour obtenir ce résultat, Bessel a mesuré un angle d’environ 1/10 000 de degré, un exploit technique pour l’époque!

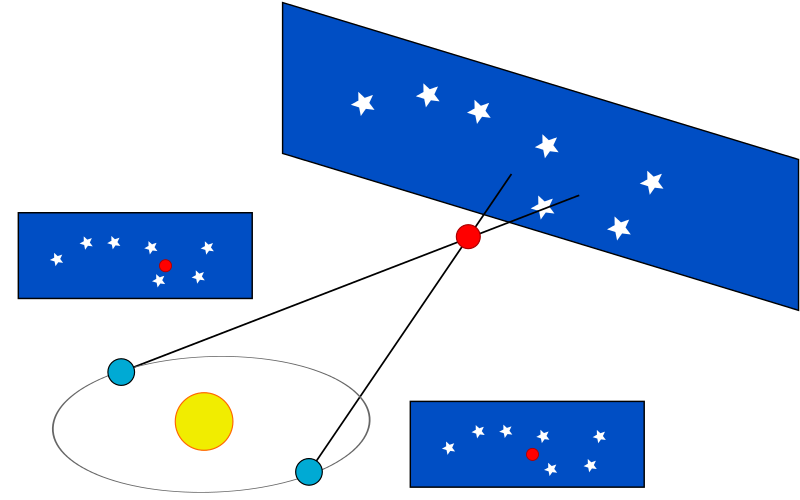
La méthode de la parallaxe permet de mesurer précisément la distance des étoiles les plus proches. Le satellite européen Hipparcos a mesuré la distance de 118 218 étoiles entre 1989 et 1993. La précision des mesures d’angle est d’environ 10 millionièmes de degrés et le satellite a été en mesure de déterminer la distance d’étoiles avec une incertitude inférieure à 10% jusqu’à environ 1000 années-lumière. Au-delà de 1000 années-lumière, l’incertitude devient très importante et la méthode de la parallaxe ne peut pas être utilisée pour déterminer adéquatement les distances.

Méthodes basées sur l’intensité et la luminosité

Si vous mettez une ampoule de 100 watts à quelques centimètres de vos yeux, elle paraîtra beaucoup plus brillante que si vous la placez à plusieurs dizaines de mètres. Cette simple observation, combinée avec une bonne compréhension de la physique de la propagation de la lumière, fournit une excellente façon de déterminer des distances. En effet, imaginez que vous connaissez le lien entre la brillance et la distance d’une ampoule de 100 watts. Si vous observez une source lumineuse et que vous savez qu’il s’agit d’une ampoule de 100 watts, vous pourrez facilement déterminer à quelle distance elle se trouve.

Luminosité et intensité

La luminosité d’une source de lumière est la quantité d’énergie que cette source émet à chaque seconde. Par exemple, une ampoule de 100 watts émet 100 joules d’énergie à chaque seconde. Une ampoule de 50 watts émet la moitié moins, soit 50 joules d’énergie à chaque seconde. La luminosité est une propriété intrinsèque à la source lumineuse qui dépend de la façon dont la lumière est produite. Dans le cas des étoiles, nous verrons la semaine prochaine que la lumière est produite par l’énergie thermique et l’énergie nucléaire. La luminosité d’une étoile dépend donc principalement de sa taille, de sa température et de sa composition chimique. Si nous connaissons ces paramètres, nous pouvons déduire la luminosité de l’étoile. À titre d’exemple, le Soleil a une luminosité de 3,8 × 10²⁶ watts. En astronomie, on utilise souvent la magnitude absolue plutôt que la luminosité. Rappelez-vous que la magnitude est une façon de mesurer la brillance d’une étoile sur une échelle où les petites valeurs correspondent à des étoiles très brillantes et les grandes valeurs à des étoiles peu brillantes. De la même façon, la magnitude absolue d’une étoile est faible si l’étoile a une grande luminosité alors qu’elle est grande si l’étoile a une faible luminosité. Le Soleil a une magnitude absolue de 4,7 alors que Deneb, une supergéante bleue environ 100 000 fois plus lumineuse que le Soleil, a une magnitude absolue de -8,7.

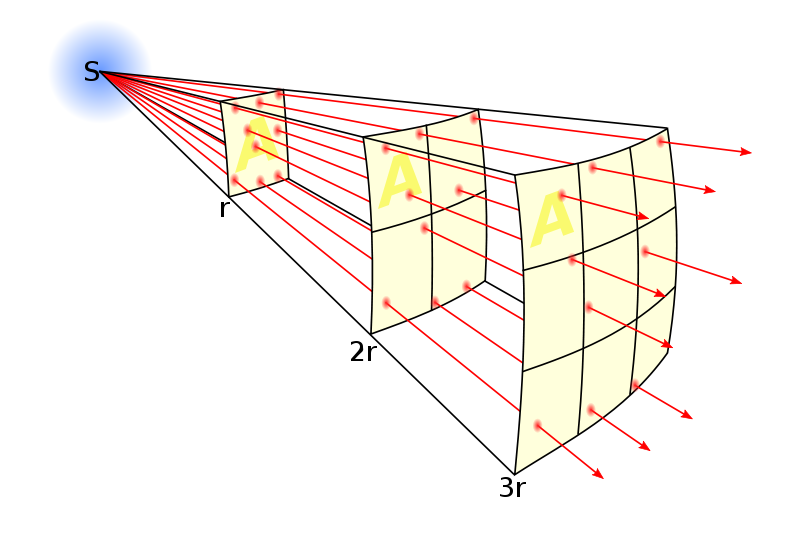
L’intensité d’une source lumineuse dépend de la distance à laquelle on l’observe. Plus la source est éloignée, moins elle est intense. L’intensité mesure la quantité d’énergie qui arrive sur chaque unité de surface d’un détecteur à chaque seconde. Par exemple, si vous lancez un caillou dans un bassin d’eau, vous verrez que la hauteur des vagues diminue à mesure que les vagues s’éloignent du point d’impact. Pourquoi? Parce que l’énergie contenue dans la vague s’est répartie sur une plus grande surface, ce qui fait moins d’énergie par unité de surface. Pour la lumière, on sait que l’intensité est inversement proportionnelle au carré de la distance de la source. La magnitude apparente dont nous avons parlé au chapitre 1 est une mesure indirecte de l’intensité.

Considérons les étoiles jumelles GSC 01799-00656 et HIP 14684. La distance de HIP 14684 a été mesurée par la méthode de la parallaxe grâce au satellite Hipparcos. Elle est de 126 années-lumière. L’étoile jumelle GSC 01799-00656 est environ 9 fois moins intense, ce qui signifie qu’elle se trouve environ 3 fois plus loin (parce que 3 au carré donne 9), soit à environ 378 années-lumière.

Type spectral

La méthode décrite ci-dessus est élégante, mais un problème important subsiste : comment fait-on pour déterminer que deux étoiles sont des «jumelles»? Il faut qu’on soit assuré que les deux étoiles sont vraiment identiques. Pour cela, nous utilisons une propriété importante de la lumière, sa couleur. La lumière est composée de plusieurs longueurs d’onde, c’est-à-dire de plusieurs couleurs. En utilisant un prisme, on peut, grâce au phénomène de la réfraction, disperser la lumière de telle sorte qu’on voit ses couleurs se séparer les unes des autres. On est alors en mesure de mesurer l’intensité des différentes couleurs et de produire un spectre de la lumière provenant de l’étoile. Il est également possible d’obtenir un spectre en utilisant un réseau de diffraction et le phénomène de diffraction. Vous pouvez facilement observer la lumière séparée en ses différentes couleurs avec un disque compact ou un DVD.

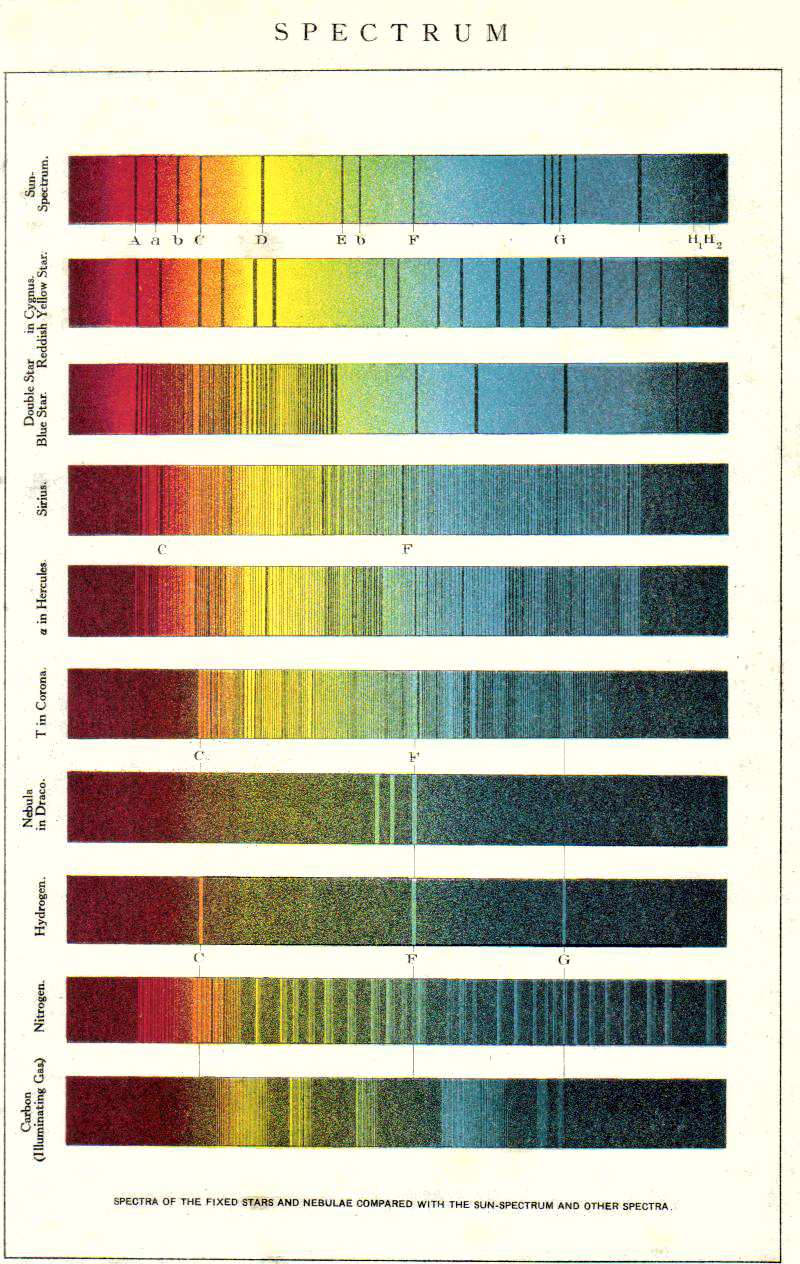
Historiquement, un appareil pour séparer la lumière (prisme ou réseau de diffraction) était installé à l’oculaire d’un télescope et le spectre était enregistré sur une plaque photographique. Ceci produisait une image en noir et blanc qui devait ensuite être comparée avec d’autres spectres manuellement. En regroupant les étoiles qui avaient des spectres semblables, on pouvait établir une classification spectrale des étoiles. À la fin du XIX^e et au début du XX^e siècle, de nombreuses étoiles ont ainsi été classifiées. Des astronomes comme Edward Pickering, Williamina Fleming, Antonia Maury et Annie Jump Cannon ont traité des dizaines de milliers de spectres ainsi.

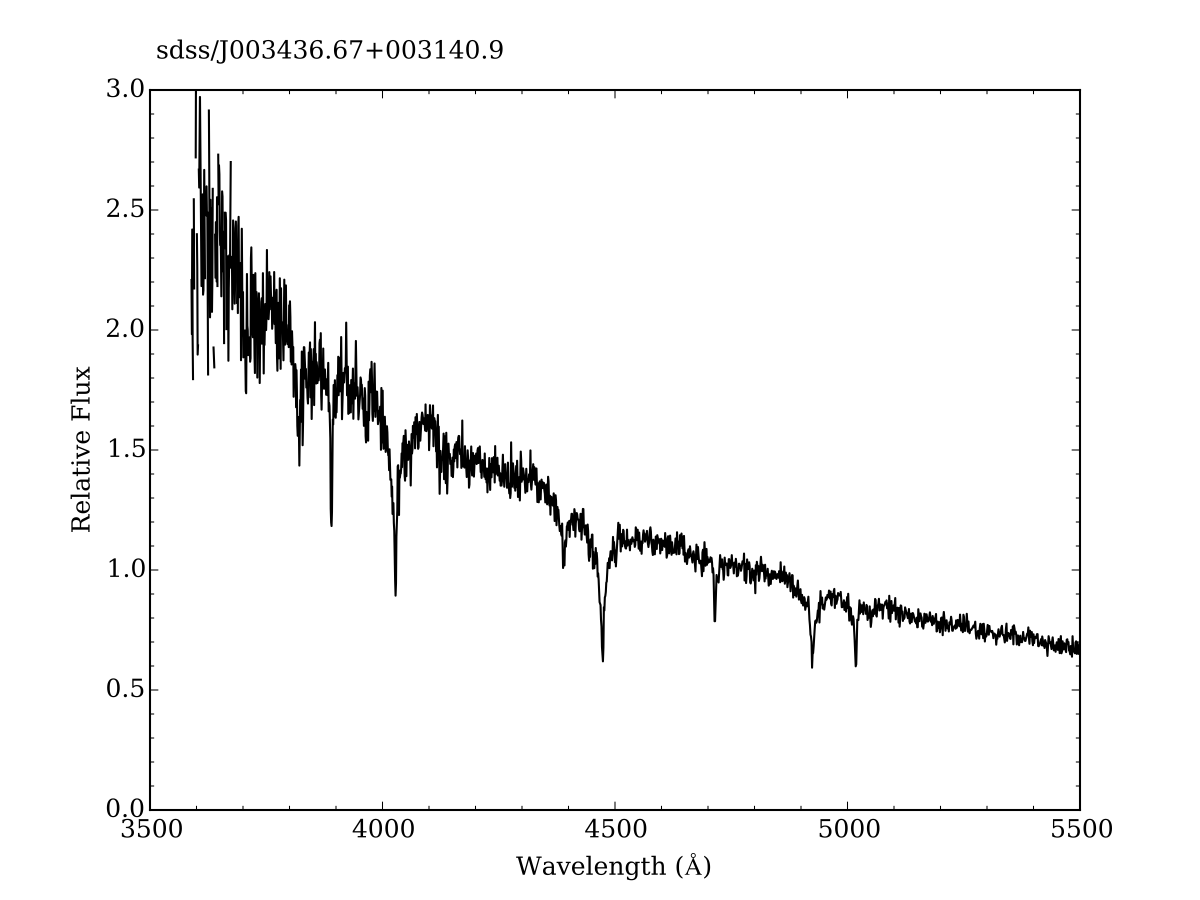
Aujourd’hui, les spectres sont enregistrés par des capteurs numériques plutôt que des plaques photographiques et ils sont traités par ordinateur. En utilisant des modèles sophistiqués et des statistiques avancées, les ordinateurs sont capables de classifier des centaines de millier de spectres rapidement.

On classe les étoiles selon leur type spectral, c’est-à-dire l’allure de leur spectre, en 9 grandes catégories identifiées par des lettres majuscules : OBAFGKMLT. Ces catégories vont des étoiles les plus bleues-blanches, celles de type O, jusqu’au étoiles rouge très foncées L et celles qui ne sont visibles que dans l’infrarouge, T. Notre Soleil, une étoile blanc-jaune, est de type G.

Deux étoiles de même type spectral et de même taille sont des étoiles jumelles. On peut donc relativement facilement trouver des étoiles jumelles en comparant leur spectre.

Céphéides

Une autre technique de mesure des distances repose sur une classe particulière d’étoiles variables qu’on appelle des céphéides. On dit qu’elles sont variables parce que leur luminosité change de façon périodique et régulière. En observant avec soin plusieurs céphéides différentes, Henrietta Leavitt a découvert, au début du XX^e siècle, que la luminosité moyenne des céphéides était proportionnelle à leur période de pulsation. Il est facile de mesurer la période de pulsation en observant l’étoile pendant quelques jours. Par la suite, grâce à la relation entre la période et la luminosité, on peut déduire la luminosité de l’étoile. Sachant sa luminosité et son intensité, on peut calculer la distance à laquelle se trouve l’étoile.

La méthode de mesure de distances basée sur les céphéides est très utile parce qu’il y a des céphéides partout dans l’Univers et que ce sont des étoiles géantes très brillantes qu’on peut donc voir à des distances énormes. En utilisant des céphéides observées par le télescope spatial Hubble, on a pu déterminer la distance de galaxies situées aussi loin que 108 millions d’années-lumière.

Résumé

Voici un résumé des méthodes de mesure de distance dont nous avons discuté dans ce chapitre et dans le chapitre 4.

Méthode	Description	Limite de distance
Radar	On envoie une onde électromagnétique vers l’astre, on mesure le temps pour que l’onde réfléchie reviennent, on déduit la distance à l’aide de la vitesse de la lumière.	Système solaire
Parallaxe	On mesure la position d’un astre par rapport aux étoiles lointaines de deux points de vue différents. En faisant un peu de trigonométrie, on déduit la distance.	Étoiles proches, jusqu’à ~1000 années-lumière
Étoiles jumelles	On connaît la distance d’une étoile A. On trouve une étoile B qui a un spectre presque identique. Ces étoiles ont la même luminosité (et donc la même magnitude absolue). On mesure l’intensité (ou la magnitude apparente) des deux étoiles. En utilisant la relation entre la luminosité, l’intensité et la distance, on déduit la distance.	Galaxies voisines, tant que des étoiles sont suffisamment brillantes pour obtenir un spectre
Céphéides	On mesure la période de pulsation de la céphéide. Cette période permet de déduire la luminosité de l’étoile. En utilisant la relation entre la luminosité, l’intensité et la distance, on déduit la distance.	Galaxies lointaines

Exercices

1. Pourquoi ne peut-on pas utiliser la méthode de la parallaxe pour déterminer la distance des étoiles à l’autre bout de la galaxie?

2. Quelle est la différence entre la magnitude apparente et la magnitude absolue?

3. Quelle est la différence entre le phénomène de réfraction et le phénomène de diffraction?

4. On prend une ampoule de 60 watts et une ampoule de 100 watts. On place l’ampoule de 60 watts à 100 mètres. On place l’ampoule de 100 watts à 50 mètres. Laquelle des ampoules a la magnitude apparente la plus grande? Laquelle des ampoules a la magnitude absolue la plus grande? Expliquez votre raisonnement.

5. Expliquez la distinction entre intensité et luminosité.

6. Deux étoiles A et B ont la même magnitude apparente. Si l’étoile B a une luminosité 16 fois plus grande que l’étoile A et que l’étoile A est située à une distance de 20 années-lumière de la Terre, à quelle distance est située l’étoile B?

7. Deux étoiles A et B ont des spectres identiques. L’étoile A est à une distance de 100 années-lumière. L’étoile B a une intensité quatre fois plus faible que l’étoile A. À quelle distance se trouve l’étoile B?

8. La céphéide A située à 75 années-lumière a une période de 3 jours et une magnitude apparente identique à celle de la céphéide B. La céphéide B a une période de 12 jours. À quelle distance est situé la céphéide B?

9. Définissez le type spectral.

10. Les étoiles A, B et C sont jaune, bleu et rouge, respectivement. Sachant qu’il y a une étoile de type B, une étoile de type F et une étoile de type L, déterminez le type spectral de chaque étoile.