Chapitre 5 Gravitation

À la Renaissance, beaucoup de progrès ont été faits dans la compréhension de la structure du système solaire. Copernic, Galilée et Kepler ont jeté les bases d’une meilleure compréhension de l’Univers. Leurs découvertes permettaient de bien comprendre le mouvement des astres et de prédire leur position, mais elles ne fournissaient que peu d’explication quant à la raison de ces mouvements. Pourquoi les planètes tournaient-elles autour du Soleil? Pourquoi leur orbite étaient-elles des ellipses? Pourquoi la troisième loi de Kepler fonctionnait-elle aussi bien? Ce qui a permis de répondre à ces questions marque le début de la physique telle qu’on la connaît aujourd’hui.

Principe d’inertie

Galilée, en plus de ses observations astronomiques, a beaucoup contribué au développement de la physique. Il a reconnu que les objets à la surface de la Terre tombent tous vers le sol à la même vitesse, si on peut négliger toute forme de frottement, incluant la résistance de l’air. La légende veut qu’il ait laissé tomber deux boulets de masses différentes du haut de la tour de Pise pour montrer que les deux atteignaient le sol exactement au même moment. Cette réalisation importante montrait que tous les objets à la surface de la Terre étaient attirés vers le centre de la Terre de la même façon.

On doit aussi à Galilée une des premières formulations du principe d’inertie. Il a fait l’hypothèse que les objets, si on pouvait négliger le frottement, continuaient leur mouvement horizontal indéfiniment. Par exemple, un bateau voguant sur une mer sans frottement, pourrait, si on lui donnait une petite poussée, faire le tour de la Terre et revenir à son point de départ. Ce principe d’inertie permettait à Galilée d’expliquer pourquoi les planètes tournaient autour du Soleil. Elles le faisaient simplement parce que ce mouvement correspondait à un mouvement «horizontal», c’est-à-dire à une distance constante du Soleil. Pour Galilée, le mouvement circulaire (ou presque) des planètes autour du Soleil s’expliquait simplement parce que c’était le mouvement «naturel».

Le philosophe français René Descartes (1596-1650) a formulé le principe d’inertie sous une forme différente. Tout comme Galilée, il reconnaissait qu’un objet qu’on mettait en mouvement conserverait son état de mouvement tant qu’il n’y avait pas de force qui agissait sur lui (frottement ou autre). La différence majeure avec la version de Galilée est que, pour Descartes, le mouvement naturel n’est pas un mouvement horizontal (ou circulaire pour un objet en orbite), mais plutôt un mouvement en ligne droite. Le principe d’inertie selon Descartes peut donc s’énoncer ainsi

Un objet en mouvement continue de se déplacer en ligne droite à vitesse constante tant et aussi longtemps qu’aucune influence extérieure n’agit sur lui.

Cette version du principe d’inertie est la même qui fut reprise par Newton plus tard et qu’on accepte comme la version correcte aujourd’hui. Le mouvement en ligne droite est dont le mouvement naturel des objets. Ceci pose cependant un problème. Si les objets ont tendance à se déplacer en ligne droite, il faut qu’une force s’exerce sur l’objet pour le placer sur une orbite circulaire. Ainsi, les planètes en orbite autour du Soleil et la Lune en orbite autour de la Terre doivent être maintenues sur ces orbites par une force, la force gravitationnelle. Cette force attractive fait en sorte que les astres s’attirent les uns les autres.

Loi de la gravitation universelle

Plusieurs scientifiques, dont Robert Hooke (1635-1703) et Christiaan Huygens (1629-1695), ont essayé de formuler une expression mathématique qui décrivait la gravité, mais ils se sont heurtés à des difficultés mathématiques importantes pour essayer de faire un lien avec les lois de Kepler. C’est Isaac Newton (1642-1726) qui y est parvenu.

Newton a récupéré plusieurs idées existantes, notamment le principe d’inertie de Descartes, et avec quelques éclairs de génie, il est parvenu a énoncé trois lois de la mécanique qui, encore aujourd’hui, peuvent être utilisées pour décrire presque toute la physique dans l’Univers. La première loi de Newton est simplement le principe d’inertie de Descartes :

Un objet en mouvement continue de se déplacer en ligne droite à vitesse constante tant et aussi longtemps qu’aucune force n’agit sur lui.

La seconde loi de Newton permet de comprendre le lien entre une force et le changement dans l’état de mouvement d’un objet. Ce que Newton a réalisé, c’est qu’une même force appliquée à deux objets de masses différentes n’avait par le même effet. Plus la masse de l’objet est grande, plus il sera difficile d’altérer son mouvement. Par exemple, il est plus difficile d’arrêter un camion qui roule à 50 km/h qu’une mouche qui va à la même vitesse. La seconde loi de Newton est la suivante :

L ’accélération subit par un corps est proportionnelle à la force nette appliquée à ce corps et inversement proportionnelle à la masse du corps.

Enfin, Newton réalisa qu’une force sur un objet ne pouvait qu’être exercée par un autre objet qui devait lui aussi subir une conséquence de cette interaction. Les forces viennent donc nécessairement en paires : la force exercée sur la rondelle par le bâton de hockey est accompagnée de la force exercée sur le bâton de hockey par la rondelle. La troisième loi de Newton, souvent appelée le principe d’action-réaction, affirme que

Toute force exercée par un objet A sur un objet B est accompagnée d’une force exercée par l’objet B sur l’objet A qui a la même grandeur et est dans la direction opposée.

Ces trois lois sont les fondements de la mécanique classique qui est encore enseignée et utilisée de nos jours. Cependant, pour qu’elles puissent être utilisées pour comprendre le mouvement des corps célestes, il fallait également une description de la force de gravité qui agissait entre ces corps. Un autre éclair de génie fit réaliser à Newton que la force qui maintient la Lune en orbite autour de la Terre est exactement la même que la force qui fait en sorte que les objets tombent vers le sol. En fait, la Lune ne fait que tomber vers la Terre, mais en raison de sa vitesse tangentielle, elle rate continuellement la Terre et continu de tomber indéfiniment. De la même façon, si on lançait un boulet de canon du sommet d’une montagne avec une vitesse horizontale suffisamment grande, le boulet de canon pourrait être mis en orbite (c’est ce qui est illustré sur la figure ci-dessous extraite des Principia de Newton).

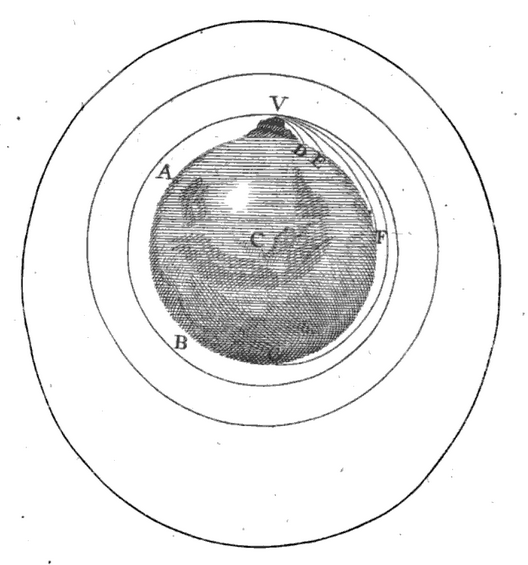
La gravité est donc une force universelle qui s’applique de la même façon aux objets à la surface de la Terre et aux corps célestes. Newton réussit également à formuler une expression mathématique pour décrire la gravitation qu’on connaît aujourd’hui sous le nom de la loi de la gravitation universelle :

\[ F_g = \frac{G m_1 m_2}{r^2} \]

Cette loi montre que la force gravitationnelle entre deux objets est une force attractive dont la grandeur est proportionnelle à la masse de chacun des deux objets et inversement proportionnelle au carré de la distance entre les objets. Si la distance entre deux objets double, la force gravitationnelle diminue d’un facteur quatre.

À partir des trois lois de la mécanique et de la loi de la gravitation universelle, Newton a été en mesure d’expliquer les lois de Kepler. L ’orbite elliptique des planètes était maintenant expliquée par les lois de Newton, de même que leur période de révolution. Pour arriver à prouver tout cela, Newton a dû inventer une nouvelle sorte de mathématiques qu’on appelle aujourd’hui le calcul différentiel et intégral (qui a été découvert simultanément par un mathématicien et physicien allemand du nom de Gottfried Wilhelm Leibniz). Newton est sans conteste un des plus grands génies de l’histoire de l’humanité. Newton a publié ses découvertes dans le livre Philosophiae Naturalis Principia Mathematica en 1687.

Succès de la mécanique newtonienne

La théorie de la gravitation newtonienne a connu un immense succès. Non seulement était-elle capable d’expliquer les observations connues, mais elle permettait de faire des prédictions qui s’avéraient exactes.

Edmond Halley (1656-1741), un contemporain et un collaborateur de Newton, a réalisé que des comètes qui avaient été observées à trois reprises dans le passé à intervalle régulier de 76 ans étaient en réalité une seule comète. Il a utilisé la théorie de la gravitation universelle de Newton pour calculer le prochain passage de cette comète de même que la légère perturbation de son orbite qui devait être causé par son passage à proximité de Jupiter. Le passage de la comète en 1758 était exactement au moment prédit par Halley.

Caroline Herschel (1750-1848) et son frère, William Herschel (1738-1822) on étudié les systèmes d’étoiles binaires et ont réalisé que les mouvements de ces étoiles concordaient parfaitement avec la théorie de Newton. Ceci confirmait que la théorie de la gravitation était bel et bien universelle et qu’elle s’appliquait à tous les objets dans l’Univers. Caroline Herschel a été la première femme a obtenir la médaille d’or de la Royal Astronomical Society.

William Herschel dans ses nombreuses observations, découvrit une nouvelle planète qu’on connaît aujourd’hui sous le nom d’Uranus. L ’astronome français Alexis Bouvard observa cette planète en détail et remarqua qu’elle se déplaçait bizarrement, déviant des prédictions de la théorie newtonienne. Une conclusion possible était que la théorie newtonienne était incorrecte. Bouvard, de même qu’une contemporaine anglaise nommée Mary Somerville, fit plutôt l’hypothèse que la perturbation de l’orbite d’Uranus était causée par une autre planète, située au-delà de l’orbite d’Uranus. John Couch Adams et Urbain Le Verrier calculèrent où devait se trouver cette nouvelle planète en se basant sur la mécanique newtonienne au début des années 1840. En 1846, l’astronome Johann Galle observa cette huitième planète à l’endroit prédit par Adams et Le Verrier. Elle fut nommée Neptune.

Toutes ces observations et bien d’autres confirment que la théorie de la gravitation universelle est une excellente théorie. On l’utilise encore aujourd’hui pour prédire la trajectoire des planètes, des satellites et des étoiles.

En science, on donne le nom de théorie à une description du fonctionnement de la nature qui a résisté à l’épreuve du temps et qui a été testée et vérifiée à répétition en utilisant la démarche scientifique. Cette définition diffère de l’usage courant du mot théorie qui sous-entend que la description sous-jacente n’est pas testée ou n’est qu’une explication possible parmi d’autres. En science, le terme correspondant est plutôt une hypothèse. Cette légère disparité entre les définitions est la cause de plusieurs erreurs d’interprétation quant à la validité des descriptions scientifiques. Par exemple, beaucoup de gens croient que la théorie quantique est hypothétique et pas nécessairement validée alors que c’est tout le contraire : la théorie quantique a résisté à tous les tests que nous lui avons fait passer et elle nous a permis de faire des progrès technologiques majeurs qui auraient été impossibles si la théorie était incorrecte.

Mauvaises nouvelles en provenance de Mercure

L ’histoire de la découverte de Neptune sembla se reproduire lorsque les astronomes observèrent en détail Mercure. Le Verrier, celui-là même qui avait calculé la position de Neptune, remarqua que la planète Mercure présentait une anomalie dans son orbite. Fort de son succès précédent, il fit l’hypothèse qu’une autre planète devait se trouver entre le Soleil et Mercure et que cette autre planète était responsable de la perturbation observée de l’orbite de Mercure. Il nomma cette planète Vulcain. Pendant des décennies, les astronomes tentèrent en vain d’observer Vulcain pour confirmer l’hypothèse de Le Verrier. Vulcain n’existait pas. Une première véritable faille dans la théorie de gravitation universelle venait d’être découverte.

Albert Einstein et la relativité

Relativité restreinte

Alors qu’il travaillait comme commis au bureau des brevets, Albert Einstein (1879-1955) réfléchissait à certains problèmes avec les théories physiques de l’époque. Une des choses qui le troublait était une incohérence entre la mécanique classique, en particulier le principe de relativité galiléen, et l’électromagnétisme, les lois qui régissent les champs électriques et magnétiques. De certains points de vue, il semblait y avoir des champs électriques alors que de d’autres points de vue, il semblait y avoir des champs magnétiques. Or, les objets portant une charge électrique sont affectés différemment par les champs électrique et magnétique. Dans la relativité galiléenne (qui avait été découverte par Galilée), les lois de la physique sont censées être les mêmes peu importe le point de vue. De plus, toutes les mesures connues à l’époque de la vitesse de la lumière donnaient exactement la même valeur, peu importe l’état de mouvement de la source ou de l’observateur. Cela contredisait directement ce qui était attendu de la relativité galiléenne.

Einstein, pour résoudre le problème, énonça deux postulats :

1. La vitesse de la lumière est la même pour tous les observateurs, peu importe leur état de mouvement.
2. Le principe de relativité galiléen est correct, c’est-à-dire que les lois de la physique sont les mêmes pour tous les observateurs, peu importe leur état de mouvement, pour autant qu’ils ne soient pas accélérés.

À partir de ces postulats, il développa ce qui est aujourd’hui connu sous le nom de la théorie de la relativité restreinte (nous verrons plus tard en quoi cette théorie est restreinte). Il publia son idée en 1905 à peu près en même temps que trois autres idées originales dans d’autres domaines de la physique alors qu’il n’avait que 26 ans. Cette théorie avait des conséquences étonnantes : le temps et l’espace devenait des grandeurs relatives, c’est-à-dire qu’elles n’étaient pas nécessairement les mêmes pour des observateurs différents. Pour un observateur en mouvement, le temps s’écoule plus lentement qu’un observateur au repos et les distances apparaissent plus courtes. Le temps et l’espace devenaient deux notions étroitement liées l’une à l’autre qu’on combina sous l’appellation commune espace-temps. Une autre conséquence est l’équivalence entre l’énergie et la masse. Un objet de masse \(m\) qui se déplace possède une énergie

\[E = \gamma mc^2\]

où \(\gamma\) est un facteur qui dépend de la vitesse de l’objet et \(c\) est la vitesse de la lumière, 300 000 km/s. Pour un objet immobile, \(\gamma\) vaut 1 et on obtient donc la relation célèbre

\[ E = mc^2\]

Ces découvertes étaient troublantes et remettaient en cause beaucoup d’éléments qui étaient pris pour acquis depuis des millénaires. Cependant, à l’instar de la mécanique newtonienne, la relativité restreinte a été vérifiée et contre vérifiée à de très nombreuses reprises. Les physiciens du début du XX^e siècle acceptèrent rapidement la proposition d’Einstein. Il est important de noter que la relativité restreinte ne rendait pas la mécanique newtonienne caduque. Les effets relativistes deviennent importants seulement lorsque les objets bougent à des vitesses proches de celle de la lumière. Dans notre expérience humaine quotidienne, tout se passe très lentement par rapport à la vitesse de la lumière et les effets relativistes sont généralement complètement négligeables. Les équations de la relativité restreinte, lorsqu’on les limite aux faibles vitesses, redonnent exactement les mêmes équations que la mécanique newtonienne. La relativité restreinte est donc une extension de la mécanique classique qui s’applique lorsque les vitesses sont très grandes. Les ingénieurs aujourd’hui utilisent principalement la mécanique classique parce que les vitesses, même celles des voitures ou des avions les plus rapides, sont infimes par rapport à la vitesse de la lumière.

Relativité générale

Quelque chose troublait cependant Einstein. Il n’aimait pas la restriction qui apparaissait dans son deuxième postulat : pourquoi l’observateur ne devait-il pas être accéléré? Pour enlever cette restriction, il dû travailler pendant onze ans! Il réalisa qu’il est impossible pour un observateur de faire la distinction entre une accélération et la gravité. Un observateur dans une fusée spatiale qui accélère à 9,8 m/s² ressentirait exactement la même chose qu’un observateur sur Terre. Les expériences qu’il ferait donnerait toutes exactement les mêmes résultats que l’observateur sur Terre. Par conséquent, s’il était enfermé dans une pièce sans fenêtre ni porte, il serait incapable de déterminer s’il se trouvait dans une fusée spatiale qui accélère ou à proximité d’un objet comme la Terre qui exerce une force de gravité. C’est ce qu’on appelle le principe d’équivalence.

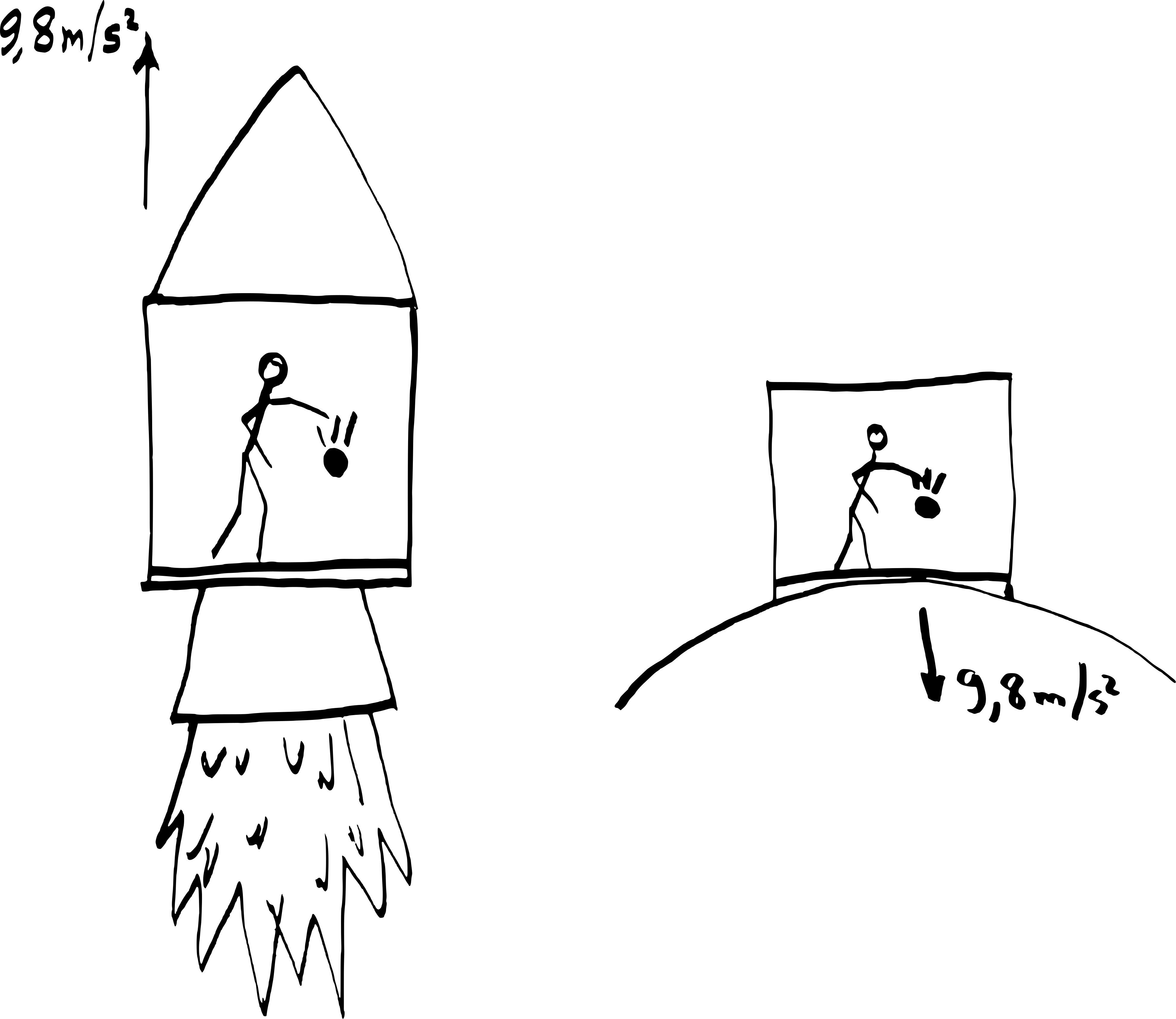
En poursuivant son raisonnement, Einstein en arriva à la conclusion que la gravité n’était pas une force à proprement parler, mais une conséquence de la déformation de l’espace-temps causé par la présence d’objets massifs. Les astres ne sont pas en orbite autour du Soleil parce que le Soleil exerce une force gravitationnelle sur eux, mais bien parce que le Soleil déforme l’espace-temps autour de lui. Les astres ne font que suivre le chemin le plus direct dans l’espace-temps (une sorte de ligne droite dans un espace à quatre dimension), mais la courbure de l’espace-temps fait en sorte qu’il décrivent une orbite. Une analogie plus facile à comprendre est d’imaginer ce qui se produirait si on se déplaçait sur Terre. Imaginez que vous marchez en ligne droite sur la surface de la Terre. Éventuellement, vous reviendrez à votre point de départ parce que la Terre est sphérique. La trajectoire que vous aurez décrite sera un cercle, même si vous aviez simplement l’impression de vous déplacer en ligne droite.

La théorie qu’Einstein développa se nomme la théorie de la relativité générale. Il la publia en 1916. Grâce à sa théorie, Einstein put calculer la forme de l’orbite de Mercure et il obtint des résultats en parfait accord avec les observations. Le problème qui avait été constaté lorsqu’on essayait de décrire l’orbite de Mercure avec la gravitation universelle de Newton était dû au fait que la courbure de l’espace-temps aussi proche du Soleil n’est pas négligeable. La relativité générale est la théorie actuelle de la gravitation. Ses prédictions ont été testées maintes fois. À titre d’exemple, le GPS qu’on utilise aujourd’hui sans trop y penser inclut des corrections dues à la relativité restreinte (les satellites bougent suffisamment vite) et à la relativité générale (la Terre courbe l’espace-temps autour d’elle). Sans ces corrections, les positions données par le GPS seraient erronées de plusieurs kilomètres.

Encore une fois, la relativité générale n’élimine pas la pertinence de la gravité universelle de Newton. Si les masses des objets impliqués ne sont pas trop importantes, la gravité universelle fait les bonnes prédictions. Ce n’est que lorsque l’on se trouve proche d’objets très massifs que la courbure de l’espace-temps devient suffisamment importante pour qu’on doive absolument en tenir compte.

Succès de la relativité générale

La théorie de la relativité générale prédit l’existence de plusieurs phénomènes exotiques. Les lentilles gravitationnelles sont celles qui ont été observées d’abord. Puisque la présence de très grandes masses courbe l’espace-temps, tout ce qui voyage dans l’espace-temps, incluant la lumière, sera affecté par cette courbure. Par conséquent, si un objet très massif, comme une galaxie, se trouve entre une source lumineuse et nous, la courbure causée par cet objet changera la trajectoire des rayons lumineux qui nous proviennent de la source. Ce changement de trajectoire fait en sorte que l’objet lumineux nous apparait à un autre endroit du ciel que celui où il se trouve réellement. Ce phénomène est analogue au changement de trajectoire que fait subir une lentille à la lumière, d’où le nom. Les lentilles gravitationnelles ont été observées pour la première fois en 1919 par Arthur Stanley Eddington. Depuis, plusieurs observations spectaculaires ont été faites comme l’image ci-dessous qui montre une galaxie rouge entre la Terre et une autre galaxie qui apparait comme un anneau bleu. En réalité, la galaxie bleue n’est pas en forme d’anneau, mais l’image qu’on en voit est déformée par effet de lentille gravitationnelle dû à la présence de la galaxie rouge.

Pour chaque corps céleste, on peut calculer une vitesse de libération qui décrit la vitesse que doit avoir un objet pour réussir à échapper à l’attraction gravitationnelle du corps céleste. Pour la Terre, cette vitesse de libération est de 11,2 km/s. Si on se trouvait à la surface du Soleil, la vitesse de libération serait de 618 km/s. À la surface d’une étoile naine blanche comme Sirius B, elle est d’environ 6700 km/s. Il est concevable que si un astre est suffisamment massif et suffisamment dense, la vitesse de libération puisse être supérieure à la vitesse de la lumière. Or, une des conséquences de la théorie de la relativité restreinte est que rien ne peut aller plus vite que la vitesse de la lumière. Par conséquent, il peut exister des objets célestes desquels rien ne peut s’échapper, pas même la lumière. On appelle de tels objets des trous noirs. Un trou noir n’est pas un aspirateur cosmique. Ce n’est pas parce qu’on est à proximité d’un trou noir qu’on est aspiré à l’intérieur. Il est tout à fait possible de rester en orbite.

Les premières observations qui suggéraient fortement l’existence d’un trou noir remontent aux années 1990. En observant comment les étoiles à proximité du centre de la Voie Lactée se déplaçaient, des scientifiques ont pu conclure qu’un objet extrêmement massif devait se trouver au centre d’une région relativement petite, conditions qui étaient difficiles à satisfaire sans la présence d’un trou noir. Les chercheurs Reinhard Genzel et Andrea Ghez qui dirigeaient deux équipes ayant fait ces observations indépendamment ont reçu le prix Nobel de physique en 2020. Récemment, en avril 2019, l’équipe internationale du Event Horizon Telescope a publié la première image d’un trou noir. Le trou noir en question se trouve au centre de la galaxie voisine de M87 dans la constellation de la Vierge. Cette image incroyable a été obtenue grâce à un radiotélescope constitué d’antennes réparties un peu partout sur la planète.

La théorie de la relativité générale prédit aussi l’existence d’ondes gravitationnelles, des vibrations dans le tissu même de l’espace-temps. Ce type d’onde est produit en grandes quantités lors d’événements extrêmes comme la collision de trous noirs ou d’étoiles à neutrons. Les ondes gravitationnelles ont été observées pour la première fois en 2016 par l’observatoire LIGO. Depuis, des dizaines d’observations ont été faites. Certains des chercheurs principaux ayant travaillé sur LIGO ont reçu le prix Nobel de physique en 2016.

Exercices

1. Quelle est la différence entre la version de Galilée du principe d’inertie et celle de Descartes.

2. Galilée avait-il besoin de la force gravitationnelle pour expliquer que les planètes tournaient autour du Soleil?

3. Quelle observation importante Ptolémée essayait-il d’expliquer en introduisant l’équant et la Terre décentrée dans son modèle du système solaire?

4. On applique la même force aux objets suivants : une voiture, une pomme, le stade olympique, une fourmi. En utilisant la seconde loi de Newton, classez ces objets en ordre croissant de l’accélération qu’ils subiront.

5. On laisse tomber les objets suivants en même temps du haut d’une tour : une voiture, une pomme, une fourmi. Classez ces objets dans l’ordre où ils frapperont le sol.

6. Présentez deux observations faites après la publication de la mécanique newtonienne qui venait confirmer la validité de cette théorie.

7. Quelle était l’importance historique de l’observation de montagnes sur la Lune par Galilée?

8. Associez les noms suivants aux découvertes correspondantes. Noms : Urbain Le Verrier, Albert Einstein, René Descartes, Isaac Newton, Caroline Herschel, Johann Galle. Découverte : Principe d’équivalence, étude des étoiles binaires, observation de Neptune, principe de l’inertie, gravitation universelle, calcul de la position de Neptune.

9. Bob vous dit qu’il a observé à plusieurs reprises que lorsqu’il y a des nuages, il pleut. Il pense donc que la présence de nuages est associée à la pluie. Alice vous dit qu’elle a étudié le processus de condensation de la vapeur d’eau en laboratoire, qu’elle a élaboré des équations qui prédisent la température à laquelle la vapeur d’eau condense, qu’elle a utilisé ces équations pour prédire la hauteur à laquelle les nuages ont tendance à se former et qu’elle a confirmé par l’observation qu’ils se formaient bel et bien à cette hauteur. Entre Bob et Alice, qui a développé ce qui se rapproche le plus d’une théorie scientifique? Qui a développé ce qui se rapproche plus d’une hypothèse scientifique?

10. Décrivez, schéma à l’appui, la méthode d’Ératosthène pour mesurer la circonférence de la Terre.

11. Imaginez Isaac dans un train qui avance à 50 km/h. Albert est assis sur un banc de parc, regarde le train passer et voit Isaac par la fenêtre. Isaac lance une balle vers l’avant du train et voit la balle s’éloigner de lui à 5 km/h. À quelle vitesse Albert voit-il la balle avancer?

12. Imaginez Isaac dans un train qui avance à 1000 km/s. Albert est assis sur un banc de parc, regarde le train passer et voit Isaac par la fenêtre. Isaac envoie un signal lumineux vers l’avant du train et voit le signal s’éloigner de lui à 300 000 km/s. À quelle vitesse Albert voit-il le signal lumineux avancer?

13. Dans la théorie de la relativité générale, pourquoi les planètes sont-elles en orbite autour du Soleil?

14. Qu’est-ce que la vitesse de libération? Pourquoi la vitesse de libération à la surface du Soleil est-elle plus grande que celle à la surface de la Terre?

15. Placez les phases de la Lune suivante en ordre en commençant par la nouvelle Lune : nouvelle Lune, gibbeuse décroissante, premier quartier, dernier croissant, pleine Lune, premier croissant, gibbeuse croissante, dernier quartier.