Chapitre 3 Astronomie à la Renaissance

Le modèle géocentrique de Claude Ptolémée a été accepté pendant plus de mille ans. Il a fallu attendre le début de la Renaissance pour qu’un nouveau modèle soit présenté. Ce nouveau modèle, introduit par l’astronome polonais Nicolaus Copernicus a révolutionné l’astronomie et a permis de faire de grandes avancées dans notre compréhension de l’Univers.
Système héliocentrique de Copernic
Nicolas Copernic (1473-1543) était un intellectuel qui, à l’instar de plusieurs de ses contemporains, ne se limita pas à l’étude d’une seule discipline. Il étudia les mathématiques et l’astronomie, mais aussi l’économie et la médecine. Il occupa plusieurs positions administratives et politiques. Il fit des observations astronomiques détaillées et précises, mesurant entre autres les positions des planètes avec des erreurs de moins d’un demi-degré.

Sa motivation à concevoir un modèle différent de celui de Ptolémée était probablement en grande partie liée à un principe d’élégance des mathématiques et de simplicité. Le modèle de Ptolémée, avec ses équants, ses épicycles et ses contraintes étranges sur un grand nombre de paramètres semblait trop complexe. Son inconfort avec le modèle de Ptolémée l’amena à concevoir un Univers complètement différent. Il plaça le Soleil au centre de l’Univers et les planètes, de même que la Terre, en rotation autour du Soleil. On dit qu’il s’agit d’un modèle heliocentrique. Il enlevait à la Terre sa position particulière et faisait d’elle une planète comme les autres. La Lune demeurait en orbite autour de la Terre. Il détermina l’ordre des planètes en se basant sur la période sidérale, de chacune, c’est-à-dire le temps qu’elle prenait pour faire le tour du Soleil. Les planètes qui tournaient autour du Soleil en moins de temps devaient être plus proches alors que celles qui tournaient en plus de temps devaient être plus loin. À partir du Soleil, les planètes sont Mercure, Vénus, la Terre, Mars, Jupiter et Saturne. Toujours influencé par la tradition grecque, les orbites des planètes dans son modèles sont circulaires. Copernic reconnait que les étoiles sont beaucoup plus loin de la Terre que ne l’est le Soleil et les place sur une sphère immobile. Ainsi, le mouvement apparent de la sphère céleste n’est pas dû à un mouvement réel de la sphère, mais plutôt à un mouvement de la Terre elle-même. Copernic reconnait même que la Terre a deux mouvements distincts, sa rotation sur elle-même et sa révolution autour du Soleil.

Le modèle de Copernic explique directement le mouvement rétrograde des planètes de même que la taille relative des rétrogradations. Lorsque la Terre tourne sur son orbite, elle rattrape éventuellement Mars qui est sur une orbite plus longue. Par conséquent, la ligne de visée qui va de la Terre vers Mars donne une projection de Mars sur la sphère céleste qui a un mouvement apparent rétrograde. C’est ce qui est illustré sur la figure de gauche ci-dessous. Dans le modèle de Copernic, les planètes tournent toujours dans le même sens. Ceci est beaucoup plus simple que l’explication du mouvement rétrograde avec les épicycles du modèle de Ptolémée (illustré à droite ci-dessous). Les planètes Jupiter et Saturne font un mouvement rétrograde relativement plus petit que celui de Mars simplement parce qu’elles sont plus éloignées de la Terre.
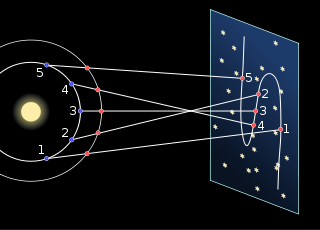
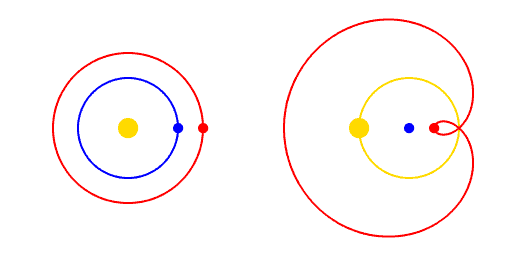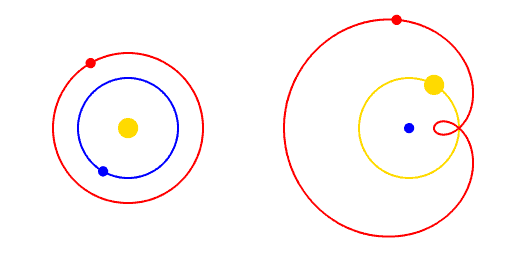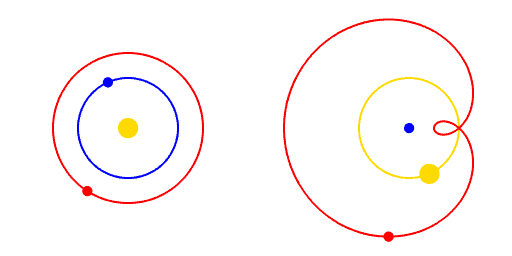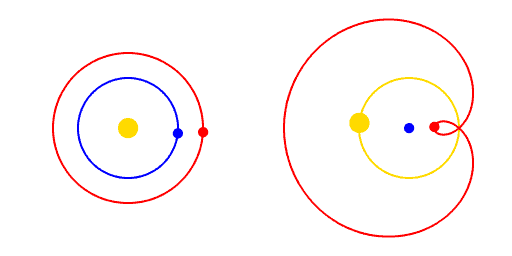
Cependant, tout n’allait pas à la perfection dans le modèle de Copernic. Il n’arrivait pas à expliquer la préférence zodiacale. Pour régler ce problème, il introduisit des épicycles qui avaient pour effet de décentrer les orbites des planètes par rapport au Soleil. Cet ajout rendait le modèle plus complexe et réutilisait le vieux concept des épicycles. Il fallut attendre Johannes Kepler, quelques décennies plus tard, pour régler ce problème.
Copernic publia ses résultats et son modèle l’année de sa mort, en 1543. Son livre, De Revolutionibus Orbium Coelestium fut accueilli plutôt favorablement, même par les autorités religieuses. Plusieurs y voyaient une nouvelle méthode mathématique pour modéliser les mouvements des astres, mais ne concevaient pas encore qu’il puisse s’agir d’une vraie description de la réalité.
Fait à noter, même si le modèle de Copernic était plus proche de la réalité que celui de Ptolémée, les prédictions qu’il permettait de faire n’était pas plus précises. En effet, comme le modèle de Ptolémée, le modèle de Copernic permettait de prédire la position des astres avec une précision de l’ordre de 5°.
Observations de Galileo Galilei
Galilée (1564-1642) était un astronome et un physicien italien qui a contribué à l’acceptation du modèle de Copernic et au développement de la cinématique et de la mécanique. Il était également doué pour l’ingénierie et il développa plusieurs appareils qui eurent un certain succès commercial (notamment des compas et des télescopes). Il fut pendant une bonne partie de sa vie en bons termes avec les autorités religieuses. Cependant son engouement public pour le modèle héliocentrique de Copernic lui valut éventuellement un procès et une condamnation à la prison à vie pour «suspicion d’hérésie». Il purgea sa peine en étant assigné à sa résidence pour le reste de sa vie. Son ouvrage Dialogo sopra i due massimi sistemi del mondo fut mis à l’index. En 1992, le pape Jean-Paul II reconnu que l’église catholique avait mal traité Galilée et exprima des regrets pour la façon dont le dossier fut traité.

Grâce à ses télescopes, Galilée put faire plusieurs observations qui supportaient le modèle de Copernic.
Lunes de Jupiter
Avant Galilée, personne ne pensait qu’il existait des satellites naturels autour d’autres planètes que la Terre. La Lune était le seul satellite naturel connu et le fait que la Terre possédait un satellite était un gage de la position particulière que notre planète devait occuper dans l’Univers. De plus, l’hypothèse prédominante était qu’une planète en mouvement ne pourrait pas conserver des lunes en orbite, ces lunes se perdraient éventuellement dans l’espace. Comme la Terre était immobile au centre, la Lune pouvait tourner autour de la Terre sans problème. Avec son télescope, Galilée découvrit que Jupiter avait également des lunes. Les quatre plus grosses lunes de Jupiter, Io, Europe, Ganymède et Callisto sont aujourd’hui nommées les lunes galiléennes et l’honneur de cette découverte. Il put observer le mouvement de ces lunes autour de leur planète. L ’image ci-dessous, prise avec un télescope moderne, montre les quatre lunes galiléennes.

Dans le modèle de Copernic, les lunes sont simplement sur des orbites autour de leur planètes qui sont elles-mêmes en orbite autour du Soleil. L ’idée selon laquelle une planète ne pouvait garder ses lunes si elle était en orbite était contredite par l’existence des lunes de Jupiter. La place particulière de la Terre était également ébranlée : d’autres planètes pouvaient aussi avoir des lunes.
Phases de Vénus
Vénus est une planète inférieure. Dans le modèle de Ptolémée, pour expliquer le fait qu’elle n’est jamais bien loin du Soleil, il fallait que le centre de son épicycle soit toujours sur l’axe Terre-Soleil. Or, si c’était le cas, on ne verrait jamais complètement la face éclairée de Vénus parce qu’elle se trouverait toujours entre la Terre et le Soleil. Galilée a observé les phases de Vénus avec son télescope et s’est aperçu qu’on pouvait voir toutes les phases de Vénus, incluant une Vénus pleinement éclairée. Ces observations concordent très bien avec le modèle copernicien, mais pas du tout avec le modèle de Ptolémée.
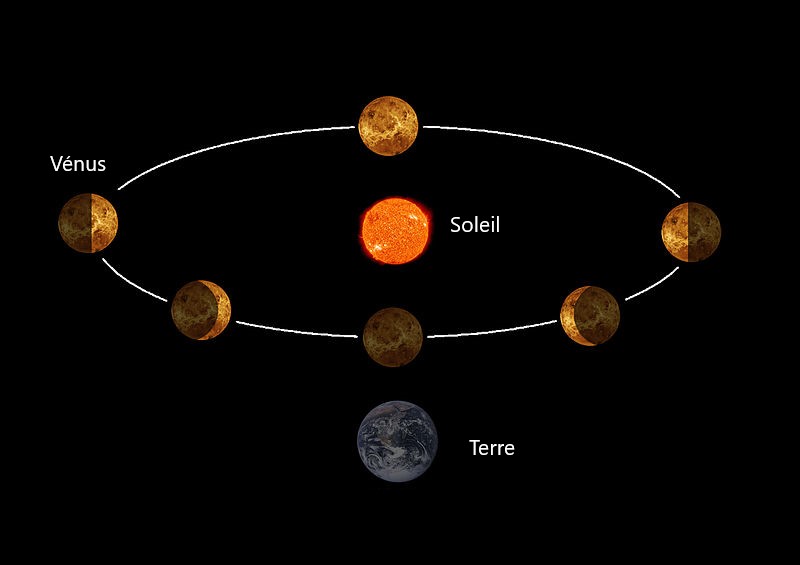
Montagnes sur la Lune
Galilée a également observé des montagnes sur la Lune. Ces montagnes, clairement visible grâce aux ombres qu’elles projettent, sont des structures semblables à celles qu’on retrouve sur Terre. La Lune est donc un objet similaire à la Terre et est malgré tout en mouvement. Ceci supporte l’idée que la Terre soit en mouvement, même si elle nous parait très grosse et difficile à bouger.

Taches solaires
Des taches plus sombres apparaissent et disparaissent de la surface du Soleil. Ces taches bougent à la surface. L ’observation de ces taches par Galilée montrait que le Soleil n’était pas un objet éternel et immuable : il changeait, tout comme les choses sur Terre. Cela remettait en question l’hypothèse selon laquelle tout ce qui se trouvait dans les cieux était figé à tout jamais. L ’Univers semblait être beaucoup plus dynamique que ce qui était accepté avant Galilée.

Tycho Brahe et Johannes Kepler
Tycho Brahe (1546-1601) était un contemporain de Galilée. C’était un Danois fort habile pour prendre des mesures astronomiques précises. Le roi danois Frédérick II a donné a Tycho Brahe un observatoire astronomique sur l’île de Hven : Uraniborg. En utilisants des instruments somme toute rudimentaire (il n’avait pas de télescope contrairement à Galilée) il mesura la position des astres avec une précision exemplaire (de l’ordre du soixantième de degré). En utilisant la technique de la parallaxe, dont nous parlerons dans un chapitre ultérieur, il était capable de déterminer quels objets célestes étaient les plus éloignés. Il observa qu’il était incapable de mesurer la parallaxe des étoiles ce qui pouvait signifier deux choses : soit les étoiles étaient beaucoup plus loin que ce que les gens de l’époque imaginait, soit la Terre était immobile. Tycho Brahe opta pour la deuxième hypothèse et développa un modèle du système solaire où la Terre était au centre mais dans lequel certaines planètes tournaient autour du Soleil plutôt qu’autour de la Terre.

Johannes Kepler (1571-1630) était l’assistant de Tycho Brahe. À la mort de Brahe, il a hérité de son poste de mathématicien impérial et il a entreprit d’analyser en détail les données qu’il avait amassé avec Brahe. Contrairement à son patron, Kepler était convaincu de la validité du modèle de Copernic. Féru de mathématiques, il a découvert dans les données trois lois qui régissent le mouvement des astres. Ces lois corrigeaient légèrement le modèle de Copernic et permettaient d’expliquer beaucoup plus élégamment la préférence zodiacale et de fournir des prévisions beaucoup plus précises de la position des astres.

Première loi de Kepler
Les planètes tournent autour du Soleil le long d’orbites en forme d’ellipse et le Soleil se trouve à un des foyers de ces ellipses.
Cette découverte est majeure. Pour la première fois depuis les Grecs anciens, un modèle du système solaire laisse tomber la figure du cercle pour les orbites des planètes.
Une ellipse ressemble à un cercle aplati. Le plus grand diamètre s’appelle le grand axe, ou axe majeur, et le plus petit le petit axe, ou axe mineur. Une ellipse a deux foyers qui peuvent être confondus (dans le cas d’un cercle) ou très éloignés dans le cas d’une ellipse très aplatie. L ’excentricité d’une ellipse mesure son aplatissement. Une ellipse avec une excentricité de zéro est un cercle, une ellipse avec une excentricité près de 1 est très plate.
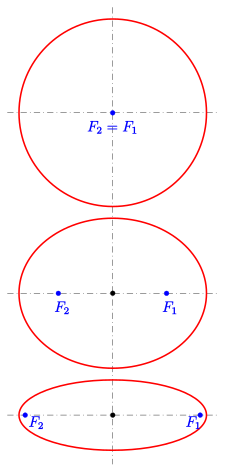
Grâce aux données de Brahe, Kepler a été en mesure de déterminer l’excentricité des orbites des planètes connues. Il s’avère que certaines planètes, comme Vénus, ont une excentricité presque nulle et se trouvent donc sur des orbites circulaires. Par contre, d’autres planètes ont des excentricités beaucoup plus importantes. Mercure, par exemple, a une excentricité de 0,206.
Deuxième loi de Kepler
Le segment de droite qui relie une planète au Soleil balaie des aires égales en des temps égaux.
Cette loi signifie que les planètes se déplacent plus rapidement lorsqu’elles sont plus proche du Soleil. Kepler ne fournit pas d’explication valide pour ce phénomène, il fallut attendre Newton pour obtenir une explication physique valide.
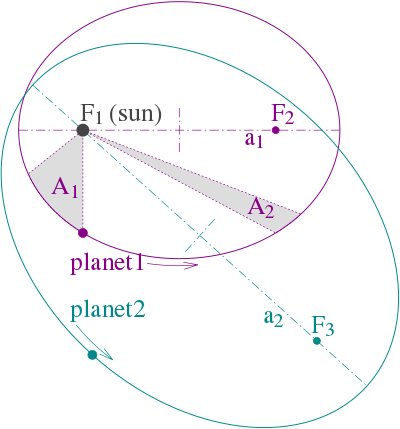
Cette loi permet d’expliquer la préférence zodiacale. Quand la planète est plus loin du Soleil (à sa position qu’on appelle aphélie) elle va plus lentement donc elle reste plus longtemps face aux constellations correspondantes. À sa position la plus proche du Soleil, le périhélie, la planète va plus vite et reste donc moins longtemps vis-à-vis des constellations de cette région du ciel.
Troisième loi de Kepler
Le carré de la période sidérale d’une planète est proportionnel au cube du demi-grand axe de son orbite.
Cette loi, plus mathématique, dit essentiellement que plus une planète est loin du Soleil, plus le temps requis pour faire le tour du Soleil est long. Ceci concorde parfaitement avec le fait que les planètes proches du Soleil comme Vénus et Mercure ont des périodes sidérales de moins d’un an alors que les planètes plus loin du Soleil comme Saturne et Jupiter ont des périodes de quelques dizaines d’années.
Exercices
Comment le modèle de Copernic explique-t-il le mouvement rétrograde des planètes?
Expliquez trois différences entre le modèle de Ptolémée et le modèle de Copernic.
Quelle idée chère aux Grecs anciens Copernic conserva-t-il dans son modèle?
Tracez les lignes de visées qui vont de la Terre à une planète supérieure à différents moments pour illustrer comme le mouvement rétrograde est expliqué dans le modèle de Copernic.
Vrai ou faux? Le modèle de Copernic permettait de faire des prédictions de la position des planètes beaucoup plus précises que le modèle de Ptolémée.
Nommez quatre observations de Galilée et expliquez en quoi elles supportaient le modèle de Copernic.
Définissez l’excentricité d’une ellipse.
Énoncez les trois lois de Kepler.