Chapitre 4 Distances dans le système solaire

Plusieurs éléments du dernier chapitre devraient vous avoir laissé un peu perplexe. Dans le modèle de Copernic, le Soleil est beaucoup plus loin de la Terre que ne l’est la Lune. Mais alors, pourquoi la Lune apparaît-elle aussi grosse que le Soleil dans le ciel? Kepler, pour énoncer sa troisième loi, devait connaître la grandeur de l’axe majeur des différentes planètes, mais comment pouvait-il déterminer ces grandeurs? Il s’avère que déterminer les grandeurs des objets et les distances entre ces objets est un des problèmes fondamentaux de l’astronomie. C’était vrai à la renaissance et c’est encore vrai aujourd’hui. Dans ce chapitre nous verrons quelques techniques qui permettent de déterminer la grandeur des objets dans le système solaire de même que la distance entre ces objets. Nous discuterons de techniques anciennes, mais aussi de certaines méthodes modernes.
Aristarque, le Soleil et la Lune
Le Soleil et la Lune ont la même taille apparente dans le ciel terrestre soit une taille angulaire d’environ 0,5°. Cette observation ne permet cependant pas de savoir si le Soleil et la Lune ont la même taille et sont à la même distance de la Terre, ou si un des deux est plus grand, mais se trouve plus loin de la Terre. Au IIIe siècle avant J.-C. L ’astronome grec Aristarque de Samos a conçu une technique pour déterminer la distance relative de ces deux astres. L ’idée repose sur la trigonométrie, branche des mathématiques qui étudie les liens entre les grandeurs des côtés des triangles et les angles intérieurs de ces triangles.
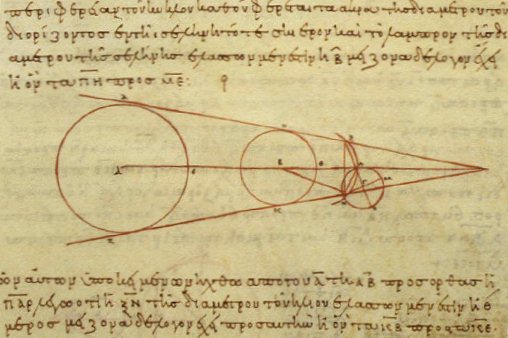
Les rapports des côtés d’un triangle rectangle, c’est-à-dire un triangle ayant un angle de 90°, définissent les rapports trigonométriques sinus, cosinus et tangente. L ’image ci-dessous montre un triangle rectangle de côtés \(a\), \(b\) et \(c\), un des angles de ce triangle et les définitions du cosinus et du sinus de cet angle. Le lien qui relie les carrés des grandeurs de côtés est connu sous le nom du théorème de Pythagore.
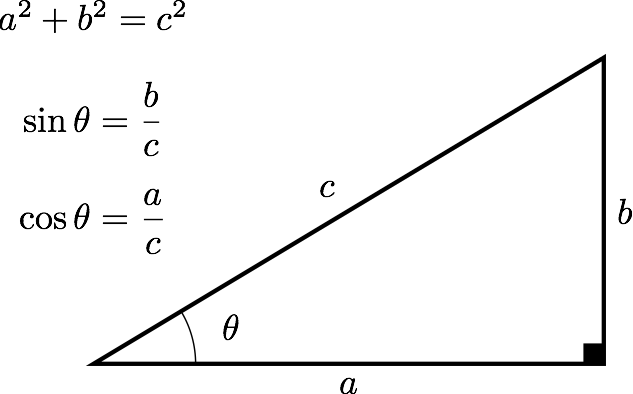
Lorsque la Lune est en premier quartier ou en dernier quartier, le segment de droite qui relie la Lune à la Terre arrive directement sur la frontière entre la partie éclairée et la partie sombre de la Lune. Cela signifie que ce segment de droite fait un angle de 90° avec le segment de droite qui relie la Lune au Soleil. En ajoutant le segment de droite qui relie la Terre au Soleil, on obtient donc un triangle rectangle. Ainsi, en mesurant l’angle entre la Lune et le Soleil lorsque la Lune est en premier ou en dernier quartier, on peut obtenir le rapport de la distance Terre-Lune (\(a\) dans le schéma ci-dessous) sur la distance Terre-Soleil (\(b\) dans le schéma ci-dessous). Aristarque de Samos mesura un angle de 87°, ce qui lui permettait de conclure que le Soleil était environ 19 fois plus loin de la Terre que ne l’était la Lune. L ’angle obtenu par Aristarque n’était pas tout à fait correct et on sait aujourd’hui que cet angle est en réalité de 89,85° ce qui signifie que le Soleil est environ 382 fois plus loin de la Terre que ne l’est la Lune.
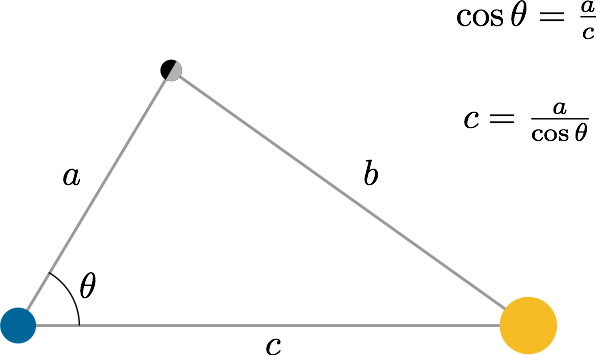
Il est important de comprendre que cette méthode ne permet pas de déterminer la distance Terre-Lune, ni la distance Terre-Soleil, mais seulement de déterminer le rapport entre ces deux quantités.
Aristarque, sachant que le Soleil était environ 19 fois plus loin que le Lune et que les deux astres avaient environ la même taille apparente, il put conclure que le Soleil devait être environ 19 fois plus grand que la Lune. Ceci est une conséquence du fait que les rapports des côtés de triangles semblables sont égaux. Avec les valeurs modernes, on sait plutôt que le Soleil est environ 382 fois plus grand que la Lune. Cette découverte d’Aristarque était importante parce qu’elle permettait d’avoir une idée de la grandeur du système solaire.
Ératosthène et la taille de la Terre
Un peu après Aristarque, Ératosthène, un autre philosophe grec, avait trouvé une méthode pour estimer la taille de la Terre. Rappelez-vous que les grecs savaient que la Terre était sphérique. Ératosthène voulait estimer la circonférence de la Terre. Pour y arriver, il mesura l’angle des rayons du Soleil par rapport à la verticale à Alexandrie au même moment où les rayons du Soleil arrivaient perpendiculairement au sol dans la ville de Syène, une ville 820 km plus au sud (voir figure ci-dessous).
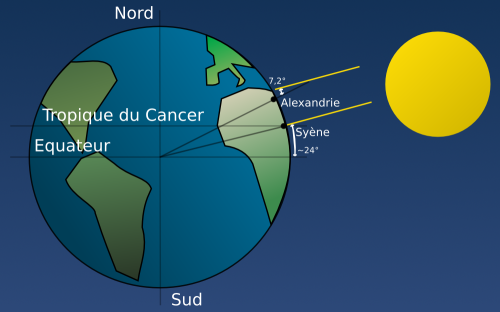
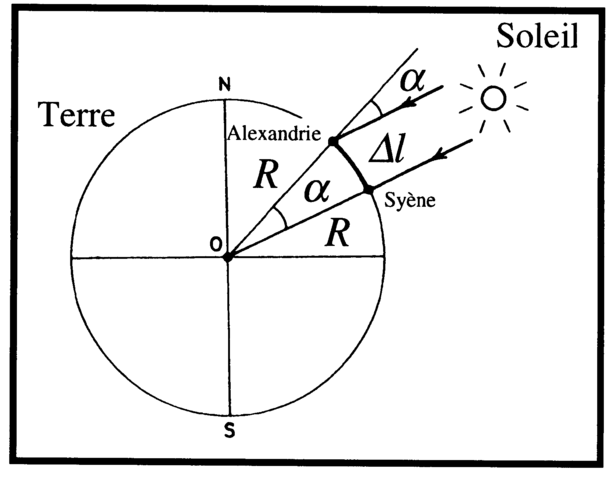
Il mesura un angle d’environ 7° grâce, encore une fois, à un peu de trigonométrie. Un peu de géométrie lui permit de conclure que l’angle de 7° était donc l’angle formé par les segments de droite reliant le centre de la Terre à Alexandrie et Syène. Sachant qu’un tour complet de la sphère terrestre équivalait à 360° et connaissant la distance entre Alexandrie et Syène, une règle de trois lui permit de déduire que la Terre avait une circonférence d’environ 42 000 km (la valeur moderne de la circonférence terrestre est de 40 000 km). Ératosthène venait d’établir la grandeur de la Terre.
Hipparque et la distance Terre-Lune
Hipparque réussit à estimer la distance entre la Terre et la Lune. Son approche reposait sur l’étude des éclipses de Lune. En supposant que le Soleil est beaucoup plus loin que la Lune, ce qui était connu depuis Aristarque, il savait que la forme de l’ombre projetée par la Terre était conique. Plus la Lune était proche de la Terre, plus elle aurait à traverser une ombre importante lors d’une éclipse de Lune. Par conséquent, l’éclipse durerait plus longtemps. Au contraire, si la Lune était loin de la Terre, l’ombre à traverser serait plus petite et alors l’éclipse durerait moins longtemps. Un peu de géométrie permit à Hipparque de calculer que la distance entre la Terre et la Lune devait être d’environ 32 diamètres terrestres. Or, le diamètre de la Terre était connu depuis Ératosthène et donc la distance Terre-Lune pouvait être estimée. On savait donc que la Lune était à environ 32 × (42 000 km / π) = 427 800 km de la Terre (la valeur moderne est 384 400 km).
En combinant ce résultat avec celui d’Aristarque, on pouvait estimer la distance Terre-Soleil à environ 19 × 1 344 000 km = 8 128 200 km de la Terre. Avec la valeur moderne du rapport distance Terre-Soleil à distance Terre-Lune, on obtient plutôt 163 419 600 km ce qui est très proche de la distance Terre-Soleil telle que mesurée aujourd’hui de 150 000 000 km.
Remarquez qu’il aurait été impossible pour Hipparque de déterminer la distance Terre-Lune sans connaître préalablement le diamètre de la Terre. Il n’aurait pu obtenir que des rapports de grandeurs, comme Aristarque. La mesure de la taille de la Terre était donc le premier pas dans la détermination de distances beaucoup plus grandes dans le système solaire. Ce mécanisme, où on se base sur une distance plus petite pour déterminer une légèrement plus grande est la base de toutes les déterminations de distances en astronomie. On y réfère souvent sous le nom de l’échelle des distances cosmique : on ne peut atteindre une distance plus grande qu’en grimpant d’abord sur le barreau correspondant à une distance plus petite.
Distance des planètes
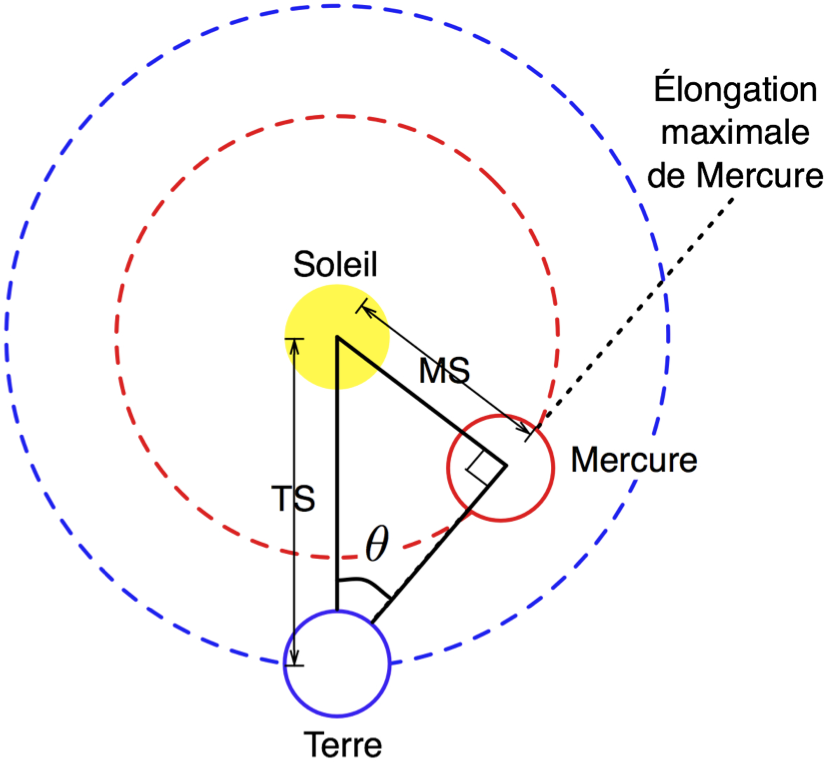
Pour déterminer les distances des autres planètes du système solaire, il fallut attendre le modèle de Copernic. En effet, ce n’est qu’avec ce modèle correct d’un point de vue géométrique qu’il était possible de concevoir des méthodes pour mesurer les distances des planètes. L ’approche pour les planètes inférieures est très similaire à celle utilisée pour déterminer la distance Terre-Lune. On considère le triangle formé par la Terre, le Soleil et la planète inférieure d’intérêt lorsque celle-ci se trouve en élongation maximale. À ce moment, l’angle à la position de la planète inférieure est un angle droit. Avec un peu de trigonométrie, on peut obtenir la distance entre la planète inférieure et le Soleil en multiple de la distance Terre-Soleil. Puisque la distance Terre-Soleil est utilisée comme valeur de référence, on la nomme une unité astronomique.
Pour mesurer les distances des planètes supérieures, Kepler proposa une technique ingénieuse basée sur l’effet parallaxe. Si on tient une pomme à quelques centimètres de son visage, la pomme n’apparait pas au même endroit par rapport aux objets lointains si on la regarde avec l’œil droit ou avec l’œil gauche. Cette disparité est utilisée par le cerveau pour déterminer la distance à laquelle la pomme se trouve. Évidemment, vous n’avez pas à faire de calculs trigonométriques complexes pour prendre une pomme, votre cerveau s’en charge. Le problème c’est que l’effet s’estompe pour les objets plus lointains. Il faudrait que nos yeux soient plus éloignés l’un de l’autre pour que l’effet parallaxe nous permette de déterminer des distances au-delà d’environ deux mètres. Les planètes supérieures sont beaucoup plus loin que deux mètres. Pour utiliser l’effet parallaxe il faut observer un objet de deux points de vue différents entre lesquels on connait la distance et il faut que cette distance soit d’une taille comparable à la distance de l’objet qu’on veut mesurer.
Kepler proposa de mesurer la parallaxe d’une planète supérieure entre deux moments où elle se trouve au même point de son orbite. À ces deux moments, la Terre est à deux endroits différents de son orbite entre lesquels on connait la distance (en unités astronomiques) puisqu’on sait combien de temps s’est écoulé entre les deux instants.
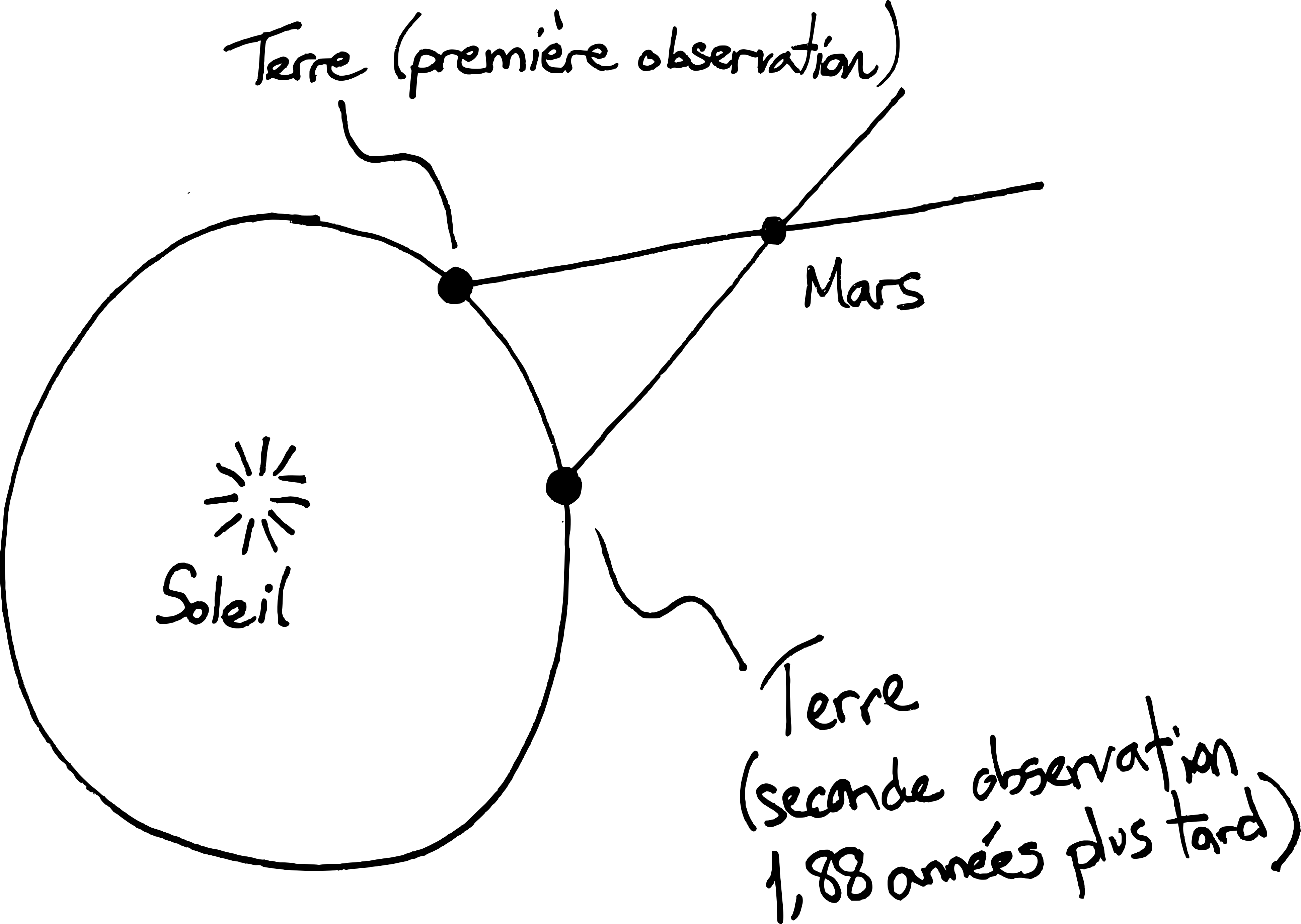
Une modification de l’idée de la parallaxe a permis de déterminer une valeur de l’unité astronomique beaucoup plus proche de la réalité que celle obtenue en Grèce antique. Entre 1671 et 1673, un scientifique italien, Giovanni Domenico Cassini, et son étudiant français, Jean Richer, ont appliqué l’idée de la parallaxe pour déterminer la valeur de l’unité astronomique. Ils ont mesuré la parallaxe de Mars depuis Paris et Cayenne, en Guyane française. Puisqu’ils connaissaient la distance entre ces deux endroits sur Terre, ils ont pu obtenir une valeur de distance de Mars. En combinant ce résultat avec la mesure de la distance Terre-Mars obtenue par Kepler en unités astronomiques, ils ont été en mesure de déduire la valeur de l’unité astronomique. À partir de ce moment, il était possible de connaître les distances de tous les astres errants dans le système solaire.
Méthode du radar
Il existe aujourd’hui une méthode beaucoup plus efficace et beaucoup plus précise pour déterminer la distance des objets du système solaire. On utilise la technique du radar. Le principe est d’envoyer une onde radio vers l’objet dont on veut savoir la distance et de mesurer le temps que prend cette onde pour atteindre l’objet et être réfléchie vers la Terre. Puisqu’on connait la vitesse de propagation des ondes radios, on peut en déduire la distance à laquelle l’objet se trouve.
Exercices
Associez chacune des personnes suivantes à une mesure de distance. Personnes : Hipparque, Kepler, Jean Richer, Aristarque, Eratosthène. Distances : détermination de l’unité astronomique, circonférence de la Terre, rapport des distances Terre-Lune et Terre-Soleil, distance Terre-Mars en unités astronomiques, distance Terre-Lune.
Qu’est-ce qu’un triangle rectangle?
Expliquez pourquoi Hipparque n’aurait pas été capable de déterminer la distance Terre-Lune sans les travaux d’Ératosthène.
Que signifie l’expression échelle des distances cosmique?
Expliquez la méthode d’Aristarque pour déterminer la distance Terre-Lune. Appuyez votre explication d’un schéma.
Énoncez la deuxième loi de Kepler et expliquez ce qu’elle signifie en termes des vitesses des planètes.
Expliquez la méthode utilisée pour déterminer la distance des planètes inférieures en vous appuyant d’un schéma.
Est-ce que la méthode que vous avez décrit à la question précédente aurait pu être utilisée avec le modèle de Ptolémée?
Définissez l’effet parallaxe.
Vrai ou faux? Une orbite avec une excentricité de 0,8 ressemble davantage à un cercle qu’une orbite avec une excentricité de 0,3.